Euler tours
22 March 2010
Introduction
The first ever paper on graph theory, written by Leonard Euler in 1736, concerned the town of Koenisberg, shown in the image below. The grey regions indicate built up parts of the town, the blue region is a river, and the black lines are bridges across the river. The question that Euler addressed in his paper was whether it is possible to walk through the town and cross each bridge once, and only once. Do you believe it to be possible?
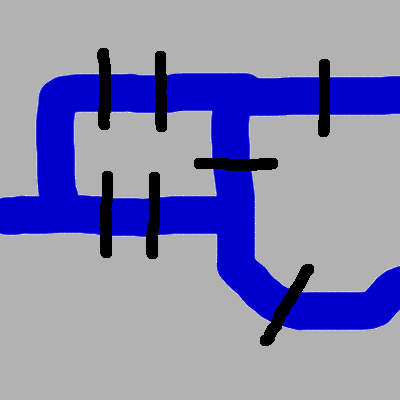
We can translate this problem into a problem about graph theory. Let us represent each grey patch of land by a (grey) vertex on a graph, and let us represent each bridge by a black edge. We obtain the graph below.
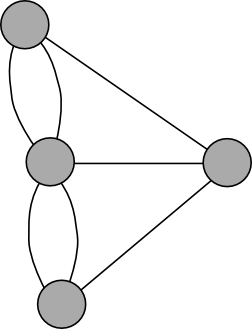
This graph differs from other graphs we have considered so far in that there are two edges between certain pairs of vertices.
A walk through a graph is a sequence of vertices v1,v2,...,vn such that vi is connected to vi+1 for each i. A path differs from a walk in that the vertices of a path must be distinct. A closed walk is a walk such that v1=vn. Euler's problem is to obtain a walk through the graph which traverses each edge once, and only once. A walk in a graph that traverses each edge once, and only once, is called an Euler trail. An Euler tour is a closed walk in a graph that traverses each edge once, and only once. Euler's question becomes does the graph shown above contain an Euler trail?
Investigation 1: Euler tours
Examine the two connected graphs shown side-by-side below. Do either of them contain Euler tours? Informally you can think of that question as follows: can you trace out all the edges of the graph, without retracing an edge more than once, such that at the end of the tracing you return to your starting point?
Using Graph Constructor, experiment with other graphs: which contain Euler tours? Examine the degrees of the vertices of graphs which do, and do not, contain Euler tours. What do you notice? Can you make a conjecture? Consider this question before moving on.
You may have the following conjecture: the connected graphs which contain Euler tours are precisely those connected graphs for which each vertex has even degree. This conjecture is true! Let us discuss one part of the conjecture, namely that if a connected graph contains a vertex of odd degree, then it does not contain an Euler tour. Try to prove this statement. Remember that for every edge coming into a vertex on an Euler tour, there must be another edge coming out of the same vertex. What does this tell you about the degree?
Investigation 2: Euler trails
In the last section we discussed the following theorem.
Theorem 1. A connected graph contains an Euler tour if and only if every vertex of the graph has even degree.
In this section we examine Euler trails. Certainly if a graph contains an Euler tour then it must contain an Euler trail; but does the reverse hold? Examine the two graphs below.
Do either of them contain Euler tours? Do either of them contain Euler trails? Notice that they contain an Euler trail if and only if the edges can be drawn without lifting one's pen from the paper or covering a line more than once. Examine other connected graphs to see if they contain Euler trails. Again, you should pay special attention to the degree of a vertex.
Every vertex other than the starting and finishing vertices of a graph with an Euler trail must have even degree. This is because for each edge of the trail leading into the vertex, there is another edge leading out of the vertex. This gives one half of the following theorem.
Theorem 2. A connected graph contains an Euler trail if and only if all but at most two of the vertices of the graph have even degree.
The part of this theorem that we have yet to prove is that a connected graph for which all but at most two of the vertices have even degree contains an Euler trail. Try to prove this statement, using Theorem 1. It will help you to imagine adding an extra edge to the graph between the starting and finishing vertices.
Finally, return to Euler's Koenisberg bridge problem, if you haven't already.
