Planar graphs
22 March 2010
Introduction
A planar graph is a graph that can be drawn in the plane in such a way that none of the edges intersect. Consider the three complete graphs below.
The complete graph with n vertices is usually denoted by Kn. The three graphs shown above are K3, K4, and K5. Which of these graphs are planar? The graph K3 is certainly planar. What about K4? It doesn't look planar; however, try dragging the bottom right hand vertex inside the triangle with corners the other three vertices. You will see that K4 is planar after all. Now experiment with K5. Can you drag the vertices around so that K5 is seen to be planar?
Remember that you are allowed curved edges in graphs. Graph Constructor doesn't allow curved edges (although you can simulate edges that turn corners by inserting tiny nodes, which we pretend to ignore, at the corners). However, there is an important result in graph theory that says that this deficiency of Graph Constructor doesn't matter. More precisely, if a graph is planar, then it can be embedded in the plane using straight line edges. So we don't need curved edges after all.
Investigation 1: K5 and K3,3
We begin by indicating why K5 is not planar. You are encouraged to fill in the details yourself. Suppose, for a contradiction, that it is planar. Consider the triangle bounded by three of the vertices A, B, and C. Consider also a fourth vertex D; this vertex either lies inside the triangle or outside the triangle. Suppose it lies in the triangle. Then we obtain the configuration shown below.
There are now four possible regions in which the fifth vertex E lies; three inside the triangle, and one outside. In each case we obtain overlapping edges.
Using Graph Constructor, click on 'select graph' and then choose 'comp bipartite' from the popup list. You will be presented with a complete bipartite graph. A complete bipartite graph is a graph for which the vertices can be split into two sets X and Y, and each vertex from X and vertex from Y are connected by an edge, but no two vertices from X, and no two vertices from Y, are connected by an edge. The complete bipartite graph for which the set X has size m, and the set Y has size n, is denoted Km,n.
We are interested in K3,3. Display this graph using Graph Constructor. Try to prove that it is not planar, using techniques similar to those above.
Neither K5 nor K3,3 can be embedded in the plane without overlapping edges. However, K5 can be embedded on the surface of a torus without overlapping edges, and K3,3 can be embedded on a Moebius strip without overlapping edges. Try to see why this is true. What is more, every graph can be embedded in three-dimensional space without overlapping edges. Imagine the nodes as little floating spheres in mid-air, with taut pieces of string connecting them.
Investigation 2: Euler's formula
A planar graph divides the plane up into distinct regions called faces. For example, each face in the blue graph below is marked by a yellow F node (F, for face).
Let us denote the number of vertices, edges, and faces of a planar graph by V, E, and F. Try calculating V-E+F for each of the planar graphs you have seen so far. What do you find? Try to prove what you find by induction.
The formula you should have found is Euler's formula V-E+F=2. Now try the following exercises. Each concerns a planar graph.
Exercise 1. Prove that 2E≥3F. (Hint: remember that each edge lies between two faces, and each face has at least three edges.)
Exercise 2. Prove that 3V-6≥E.
Using the techniques of this section try to prove, again, that K5 and K3,3 are not planar. (Hint: to deal with K3,3, first observe that K3,3 no cycles of 3 edges, and then try to obtain a stronger version of Exercise 1.)
Investigation 3: Euler's formula for polyhedra
Euler's formula V-E+F=2 also holds for a simple polyhedron, such as a cube, prism, or dodecahedron. Why is this so? It may help to revisit the nets of Platonic solids from the chapter on Hamilton cycles.
Investigation 4: Kuratowski's Theorem
The following theorem completely characterises planar graphs.
Kuratowski's Theorem. A graph is planar if and only if it contains no subdivision of K5 or K3,3.
What is a 'subdivision'? A subdivision of a graph G is a graph derived from G by adding vertices in the middle of edges from G. For example, below is a subdivision of K5. The added vertices are shown slightly smaller than the original vertices. Suppose that you start with a graph and after deleting various vertices and edges you end up with a subdivision of K5 or K3,3. Then Kuratowski's Theorem says that the graph is not planar. Conversely, if you cannot delete various vertices and edges to yield a subdivision of K5 or K3,3, then the graph is planar.
Prove that the Peterson graph, below, is not planar.
Investigation 5: map colouring
Given a map, what are the least number of colours you need to colour in different countries such that no two neighbouring countries are the same colour? Below is an image of the states of the United States of America coloured with four colours in such a way that no two neighbouring states share the same colour.
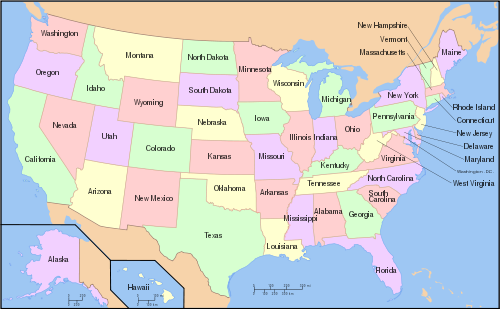
We can translate this problem into graph theory. Represent each country (or state) by a vertex. Connect two vertices by an edge if and only if the two countries (or states) are neighbours. We end up with a connected, planar graph. Our problem becomes what is the least number of colours needed to colour the vertices of a planar graph in such a way that no two neighbouring vertices are the same colour?
Let's start with a concrete case: consider the planar graph K4 displayed at the beginning of this chapter. Can you colour it with three colours as described above? What about four colours? Try to prove that any planar graph can be coloured, as described above, with six colours.
Remarkably, only four colours are needed to colour the vertices of a planar graph in such a way that no two adjacent vertices have the same colour. Below is a four-colouring of the Peterson graph. Can you colour the Peterson graph with three colours?
